Questão 01

(valor: 3,5 pontos)

Um carro está se movendo a uma velocidade constante, v = 72,0 km/h. Neste instante, no cruzamento situado a uma distância d = 40,0 m, à frente do carro, o sinal se torna amarelo e fica assim por um intervalo de tempo de 2,00 s antes de se tornar vermelho. O carro pode acelerar a no máximo 6,00 m/s² e frear a uma taxa máxima de 3,00 m/s².

a) Se o motorista frear na máxima taxa possível, calcule a posição onde o carro parará.

R: A velocidade do carro é v = 72,0 / 3,6 = 20,0 m/s. A equação de Torricelli nos dá a distância percorrida pelo carro antes de este parar: 0²=20²+2(-3,0) Dx ==> Dx = 400 / 6,00 = 66,7 m > 40,0 m. Ficaria no meio do cruzamento quando o sinal se tornasse vermelho. A distância até a segurança é de 40,0 +12,0 = 52,0 m.

__________________________________________________________________________________

b) O que o motorista deve fazer para evitar ficar exposto no cruzamento no sinal vermelho? Frear ou acelerar? Suponha que a largura total que o carro tem que atravessar no cruzamento, para que não deixe nenhuma parte exposta, é de 12,0 m.

R: No item anterior, vimos que não é uma boa estratégia frear. Se ao contrário, o carro acelerasse ao máximo, em 2,0 s ele estaria na posição x(t) dada por: x(t) = 20t + ½ (6,00) t² = 20 x 2,0 + 3,0 x 2,0 ² = 40,0 + 12,0 = 52,0 m. Ele passa pelo cruzamento em 2,0 s. A estratégia para passar pelo cruzamento será acelerar ao máximo.

Questões: 01 | 02 | 03 | demais provas

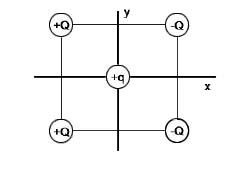
As 4 cargas ± Q da figura formam um quadrado de lado L, e a carga +q = +Q/2 está exatamente no centro desse quadrado. Sabendo que o módulo da força eletrostática entre as duas cargas +Q é F = 4,0 N no quadrado, calcule:

a) o módulo da força entre uma das cargas +Q e a carga +q;

Resposta: A força é proporcional ao produto das cargas (neste caso Qq = Q²/2) e ao inverso do quadrado da distância (neste caso 1/( Ö 2 L/2)² = 2/L²).
Assim, a força entre q e Q terá módulo KqQ/(Ö 2L/2)² = 2KQ² /2L² = 4,0 N, pois KQ² /L² = 4,0 N.

__________________________________________________________________________________

b) o módulo da força entre uma das cargas -Q e a carga +q;

Resposta: O módulo é o mesmo do caso (a): 4,0 N.
__________________________________________________________________________________

c) o módulo, a direção e o sentido da resultante das 4 forças eletrostáticas agindo sobre a carga +q.

Resposta: A força entre a carga q e uma das cargas -Q é atrativa, e entre as cargas q e +Q é repulsiva. A direção da resultante será paralela ao eixo x, pois a distribuição de cargas é a mesma dos dois lados desse eixo. O sentido será a direção positiva do eixo x, já que este é o sentido onde estão as forças atrativas. A força, e claramente o seu módulo correspondem à soma das quatro projeções de 45^o: 4x4,0x Ö 2/2 = 11,3 N.

Questões: 01 | 02 | 03 | demais provas

Questão 03

(valor: 3,5 pontos)

Um gás ideal, inicialmente a uma temperatura de 300 K e à pressão atmosférica 1atm, pode ter seu estado modificado por diferentes processos. Determine:

a) a temperatura final do gás sabendo que este gás é submetido a um processo isovolumétrico e que sua pressão final é o dobro da pressão inicial. __________________________________________________________________________________

b) a temperatura final do gás sabendo que este gás é submetido a um processo isobárico e que o volume final ocupado pelo gás é 1/3 do volume inicial. __________________________________________________________________________________

c) a razão entre os volumes final e inicial do gás, isto é ( V_final / V_inicial ), sabendo que este gás é submetido a um processo adiabático, onde a razão entre suas capacidades caloríficas é g @ 2, e sua pressão final é 1/4 da pressão inicial.

Resposta: Através da equação de estado para gases ideais, onde PV/T=nR=cte, podemos avaliar as variações sofridas pelo gás através de diversos processos.

a) Para a transformação isovolumétrica onde a modificação no gás ocorre a volume constante, temos que (P_inicial / T_inicial ) = (P_final / T_final ). Substituindo os valores dados no enunciado, temos que T_final = 600K.

b) Para a transformação isobárica onde a modificação no gás ocorre a pressão constante, temos que (V_inicial / T_inicial ) = (V_final / T_final ). Substituindo os valores dados no enunciado, temos que T_final = 100K.

c) Para a transformação adiabática, onde a modificação no gás ocorre sem a troca de calor entre o gás com seu entorno, temos que P_inicial (V_inicial)^g = P_final (V_final)^g sendo g a razão as capacidades caloríficas do gás. Substituindo os valores dados no enunciado, temos que (V_final / V_inicial )² = P_inicial / P_final = 4
Logo, temos que V_final / V_inicial = 2.

Questões: 01 | 02 | 03 | demais provas